Curl Calculator

Curl Calculator 

Find the curl of any vector in a coordinate system using the curl Calculator. It can find curl with or without points. 

How to use this tool?

The curl calculator is operated by completing the following steps.

1. Select the type of answer you want i.e. With or without points.
2. Enter the scalar functions of the 3 directions.
3. Input the value of points x,y, and z. 
4. Click Calculate.

What is the curl of a vector?

The curl of a vector field is a measure of its rotational "twisting" at any given point. It's a vector quantity that gives the axis about which the vector field rotates, as well as the magnitude of the rotation.

The idea behind the curl of a vector field is to quantify the tendency for the field to rotate about a point. 

It's like sticking a tiny paddlewheel or a windmill into the field and observing how and whether it spins. If it rotates, the vector field has a nonzero curl at that point. The axis and speed of that rotation are what the curl captures.

Mathematical Representation:

The curl of a vector field V is often denoted by ∇×V. The symbol ∇ is called the "del" or "nabla" operator and is a shorthand representation for the spatial derivatives with respect to each of the cartesian coordinates:

∇ = ( ∂/∂x i + ∂/∂y j + ∂/∂z k)

Here, i,j, and k are the unit vectors in the x, y, and z directions respectively.

Given the vector field V(x,y,z) as:

V = Pi + Qj + Rk

The curl is computed using the cross product of the nabla operator with the vector field:

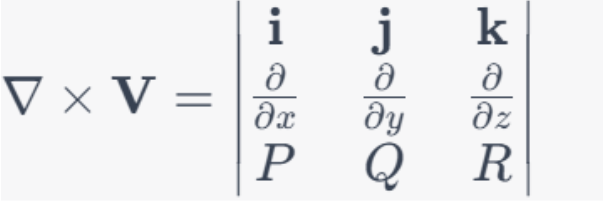
The result, as we discussed earlier, is:

How to find the curl of a vector?

To compute the curl of a vector field, you'll need to be familiar with determinants and partial derivatives. Here's a step-by-step method to find the 

Curl of a vector field V:

Given:

Let's say you have a vector field V in three-dimensional space defined by:

V = P(x,y,z)i + Q(x,y,z)j + R(x,y,z)k

Where:

• P, Q, and R are scalar functions of x,y, and z.
• i,j, and k are the unit vectors in the x, y, and z directions, respectively.

Method to Compute the Curl:

1. Write Down the Determinant Matrix:

Start by writing a 3x3 determinant with the unit vectors in the top row, the partial derivatives in the middle row, and the components of the vector field in the bottom row:

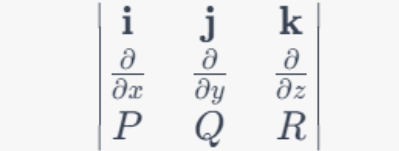
2. Expand the Determinant Along the Top Row:

• For the i component:

Multiply i by the determinant of the 2x2 matrix obtained by removing the row and column of i:

This results in  ∂R/∂y -  ∂Q/∂z.       

• For the j component:

Multiply j by the determinant of the 2x2 matrix obtained by removing the row and column of j:

This yields   ∂R/∂x -  ∂P/∂z.

•  For the k component:

Multiply k by the determinant of the 2x2 matrix obtained by removing the row and column of k:

This yields   ∂Q/∂x -  ∂P/∂y.

3. Combine the Components:

The curl ∇×V is the vector formed by combining the components we've calculated:

And there you have it! That's how you compute the curl of a vector field. The process involves setting up and evaluating a determinant with the components of the field and the partial derivatives.

Applications of Curl:

The curl of a vector field plays a significant role in multiple areas of physics and engineering. Here are some of the main applications:

• Electromagnetism: In Maxwell's equations, the curl of the electric field E is related to the rate of change of the magnetic field B, and the curl of B is related to the electric current and the rate of change of E.
• Fluid Dynamics: The curl of the velocity field in a fluid describes its vorticity, which is a measure of the fluid's local spinning or rotational motion. For example, in weather systems, vorticity is essential for understanding the formation and evolution of cyclones.
• Solid Mechanics: In the theory of elasticity, the curl of the displacement field gives the rotation field of the material points in a deformed elastic body.